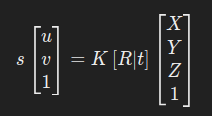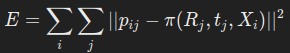fjyu95
posts tags category about
fjyu95

Contents

视觉slam

fjyu95 included in 算法知识库 Slam
   6392 words   13 minutes 

视觉slam

一个不起眼的烂笔头

视觉slam框架

整个视觉 SLAM 流程包括以下步骤。

  1. 传感器信息读取。在视觉 SLAM 中主要为相机图像信息的读取和预处理。如果是在机器人中，还可能有码盘、惯性传感器等信息的读取和同步。
  2. 视觉里程计（Visual Odometry，VO）。视觉里程计的任务是估算相邻图像间相机的运动，以及局部地图的样子。VO 又称为前端（Front End）。
  3. 后端优化（Optimization）。后端接受不同时刻视觉里程计测量的相机位姿，以及回环检测的信息，对它们进行优化，得到全局一致的轨迹和地图。由于接在 VO 之后，又称为后端（Back End）。
  4. 回环检测（Loop Closing）。回环检测判断机器人是否到达过先前的位置。如果检测到回环，它会把信息提供给后端进行处理。
  5. 建图（Mapping）。它根据估计的轨迹，建立与任务要求对应的地图。

数学基础

向量一般默认指列向量

齐次坐标

为什么要引入齐次坐标，齐次坐标的意义（一)

为什么要引入齐次坐标，齐次坐标的意义（二)

齐次坐标可以表示无穷远处的点。

齐次坐标把各种变换都统一了起来，即 把缩放，旋转，平移等变换都统一起来，都表示成一连串的矩阵相乘的形式。保证了形式上的线性一致性。

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，合并矩阵运算中的乘法和加法，简化运算操作。

内外积

点乘和叉乘

内积

数量积 点乘 一个数

/posts/algorithm_knowledge_base/7_vslam/image%201.png

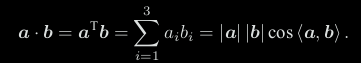
外积

向量积 叉乘 一个向量

/posts/algorithm_knowledge_base/7_vslam/image%202.png

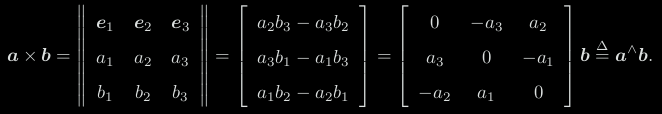
方向垂直于两个向量，大小为 |a| |b| sin ⟨a, b⟩，是两个向量张成的四边形的有向面积

把外积 a × b 写成了矩阵与向量的乘法 a∧ b，把它变成了线性运算

∧ 记成一个反对称符号，任意向量都对应着唯一的一个反对称矩阵

/posts/algorithm_knowledge_base/7_vslam/image%203.png

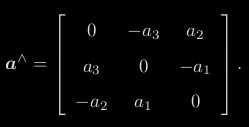
SVD分解

https://zhuanlan.zhihu.com/p/79669616

https://zhaoxuhui.top/blog/2018/03/17/SVD&SLAM.html

https://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html

1. SVD的数学形式

/posts/algorithm_knowledge_base/7_vslam/image%204.png

2. 奇异值

  • 奇异值是矩阵 A 的非负平方根，表示了矩阵在不同方向上的“重要性”或“能量”。较大的奇异值对应于矩阵中更重要的特征，而较小的奇异值则表示较不重要的特征。
  • 通过奇异值的大小，可以判断矩阵的秩、条件数以及数据的可分性。

3. 几何解释

  • SVD 的几何解释是将数据空间的线性变换可视化。矩阵 A 可以被视为将输入空间中的点映射到输出空间。通过 SVD，可以将这个映射过程分解为三个步骤：

    AA

    1. 旋转（通过 VT）将输入空间中的点旋转到新的坐标系。
    2. 缩放（通过 Σ）在新的坐标系中按奇异值的大小缩放。
    3. 再次旋转（通过 U）将缩放后的点旋转到输出空间。

应用

数据降维 PCA

矩阵近似

图像压缩

numpy scipy已实现

非线性优化

待续…

几种投影变换

仿射变换=线性变换+平移

平移、旋转、放缩、剪切、反射

https://blog.csdn.net/sgfmby1994/article/details/62426331

https://www.cnblogs.com/shine-lee/p/10950963.html

projective/perspective：三维到二维的变换

Homography：两个平面间的映射，描述同一平面在不同视角下的变换

/posts/algorithm_knowledge_base/7_vslam/image%205.png

/posts/algorithm_knowledge_base/7_vslam/image%206.png

/posts/algorithm_knowledge_base/7_vslam/image%207.png

/posts/algorithm_knowledge_base/7_vslam/image%208.png

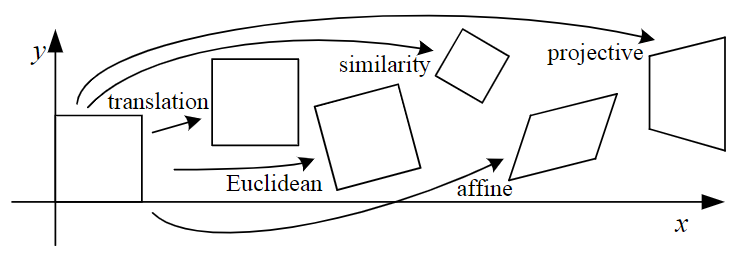
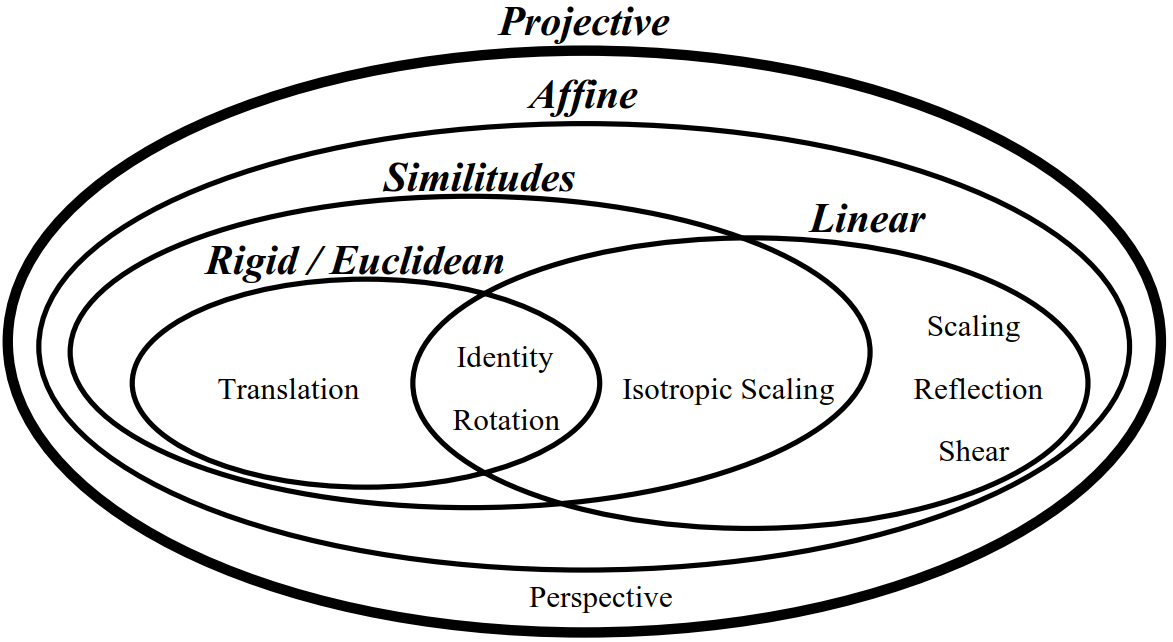
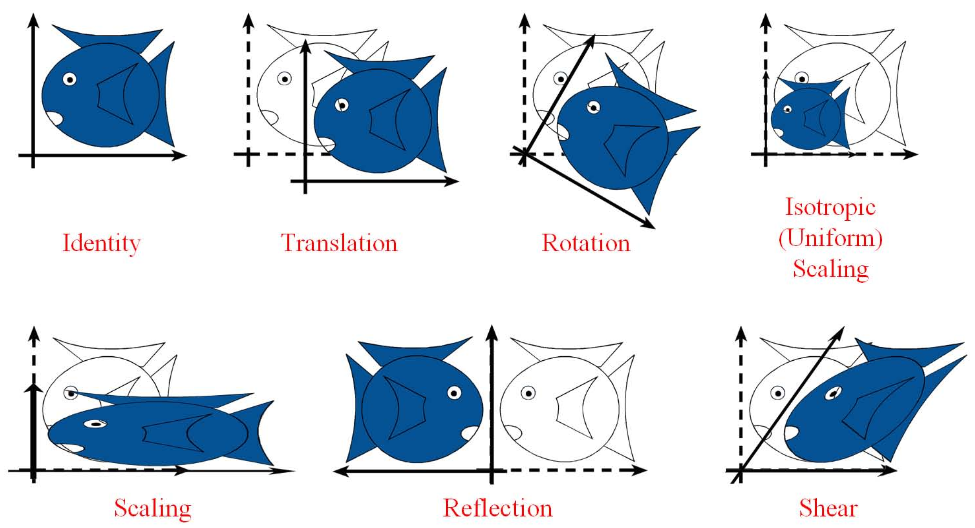
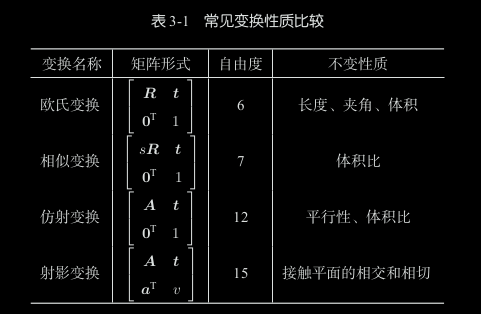
二维仿射变换是一种线性变换，保持直线性和平行性。可以进行平移、旋转、缩放、剪切等操作，常见于图像处理、计算机图形学等领域。

二维仿射变换可以用一个 3×3 的矩阵来表示：

%209.png

其中，(x,y)(x, y)(x,y) 是原始点的坐标，(x′,y′)(x’, y’)(x′,y′) 是变换后的坐标，a,b,c,da, b, c, da,b,c,d 定义线性变换（旋转、缩放、剪切等），而 tx,tytx, tytx,ty 代表平移。

三维仿射变换

三维仿射变换扩展了二维仿射变换，允许在三维空间中进行类似的操作，如平移、旋转、缩放和剪切等。它通常用 4×4 的矩阵来表示：

/posts/algorithm_knowledge_base/7_vslam/image%2010.png

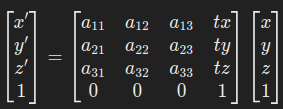
其中，(x,y,z)(x, y, z)(x,y,z) 是原始点的坐标，(x′,y′,z′)(x’, y’, z’)(x′,y′,z′) 是变换后的坐标，矩阵 aija_{ij}aij 代表线性变换，而 tx,ty,tztx, ty, tztx,ty,tz 代表平移。

三维刚体运动表示

1、旋转矩阵 不够紧凑、冗余、优化困难（带有约束）

4×4 的矩阵，将平移和旋转结合在一起，写成齐次坐标形式

/posts/algorithm_knowledge_base/7_vslam/image%2011.png

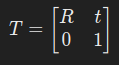
R是9个量表示3个自由度

有三个互相垂直的坐标轴（x, y, z）。旋转矩阵的 每一列 表示旋转后的坐标轴在原坐标系中的方向。

例如世界坐标系到相机坐标系的旋转变换中，旋转矩阵的列向量表示的是相机坐标系的x、y、z轴在世界坐标系中的方向。

列向量表示旋转后的基向量：

  • 旋转矩阵的每一列表示旋转后坐标轴上的基向量（单位向量）在原坐标系中的表示。
  • 例如，第一列表示旋转后x轴上的基向量在原坐标系中的坐标，第二列和第三列分别表示旋转后y轴和z轴上的基向量。

旋转角度和轴：

  • 旋转矩阵可以唯一地确定一个旋转的角度和旋转轴。
  • 通过旋转矩阵，可以计算出旋转的角度（通常使用弧度表示）和旋转轴的方向。

无奇异性

2、旋转向量 轴-角表示法

方向与旋转轴一致，长度等于旋转角**（3维向量）**

旋转向量通常表示为 r=θu，其中：

  • r是旋转向量。
  • θ是旋转角度（弧度）。例 θ=π/2
  • u是单位向量，表示旋转轴。例 u=(0.707,0,0.707)

3、欧拉角 直观

Yaw（偏航角）、Pitch（俯仰角）和 Roll（翻滚角）

万向锁问题（丢失自由度）rpy

4、四元数

既是紧凑的，也没有奇异性

没有欧拉角的万向节锁问题，适合进行连续旋转的插值计算

/posts/algorithm_knowledge_base/7_vslam/image%2012.png

/posts/algorithm_knowledge_base/7_vslam/image%2013.png

表示方法 维度 直观性 计算效率 是否有奇异性
旋转矩阵 3×3 一般 慢（9 个数） 无
欧拉角 3 直观 快 有（万向锁问题）
四元数 4 不直观 快 无
旋转向量 3 直观 快 无

相机模型

物理空间Z=1的归一化平面与像素坐标系只差一个内参矩阵K，Puv = KPc

针孔相机模型

/posts/algorithm_knowledge_base/7_vslam/image%2014.png

/posts/algorithm_knowledge_base/7_vslam/image%2015.png

/posts/algorithm_knowledge_base/7_vslam/image%2016.png

/posts/algorithm_knowledge_base/7_vslam/image%2017.png

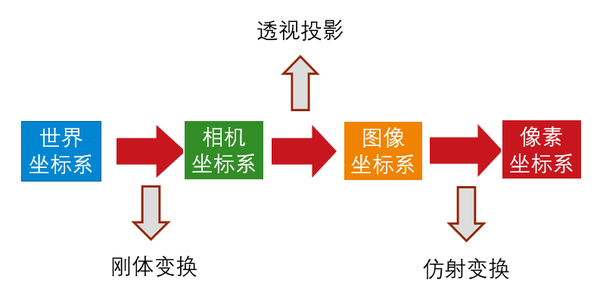
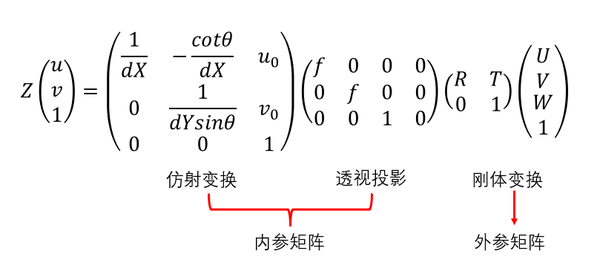
比例因子α, β 的单位为像素/米，把物理距离转换为像素距离

相机内参fx , fy代表焦距f长度对应的像素距离

主点坐标cx,cy代表相机光心在图像上的投影点位置，一般是图像的像素中心

单目相机的成像过程（针孔相机模型）：

  1. 首先，世界坐标系下有一个固定的点 P ，世界坐标为 Pw 。
  2. 由于相机在运动，它的运动由 R, t 或变换矩阵 T ∈ SE(3) 描述。P 的相机坐标为 P̃c =RPw + t。
  3. 这时的 P̃c 的分量为 X, Y, Z，把它们投影到归一化平面 Z = 1 上，得到 P 的归一化坐标：Pc = [X/Z, Y /Z, 1]T。
  4. 有畸变时，根据畸变参数计算 Pc 发生畸变后的坐标。
  5. 最后，P 的归一化坐标经过内参后，对应到它的像素坐标：Puv = KPc 。
    综上所述，我们一共谈到了四种坐标：世界坐标、相机坐标、归一化坐标和像素坐标。

双目相机

利用基线长度b、视差d来估算深度

/posts/algorithm_knowledge_base/7_vslam/image%2018.png

/posts/algorithm_knowledge_base/7_vslam/image%2019.png

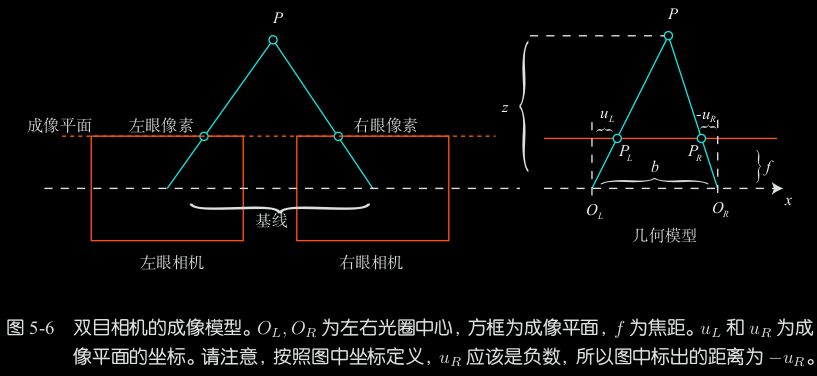
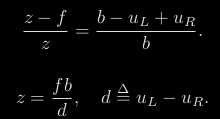
视差越小，深度越远

基线越长，测量越远

RGB-D相机 结构光、ToF

深度图转点云 相似三角形原理

/posts/algorithm_knowledge_base/7_vslam/image%2020.png

/posts/algorithm_knowledge_base/7_vslam/image%2021.png

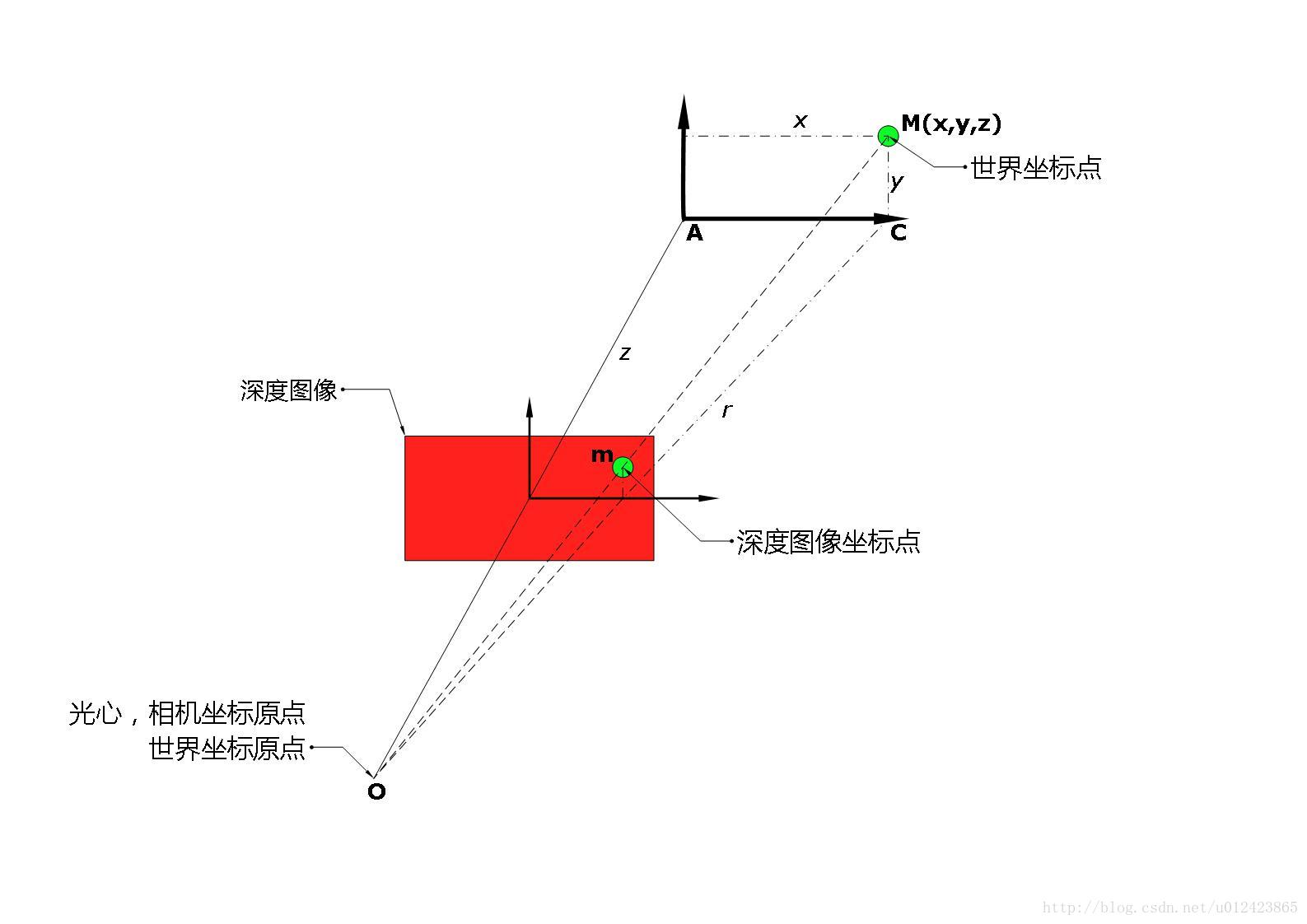
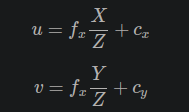
假设内参已知，知道Z的信息后，就可推算出像素坐标u,v对应的X,Y空间坐标

/posts/algorithm_knowledge_base/7_vslam/image%2022.png

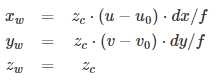
相机畸变

径向畸变

由透镜形状引起的畸变

桶形畸变和枕形畸变

/posts/algorithm_knowledge_base/7_vslam/image%2023.png

切向畸变

相机的组装过程中透镜和成像面不严格平行

/posts/algorithm_knowledge_base/7_vslam/image%2024.png

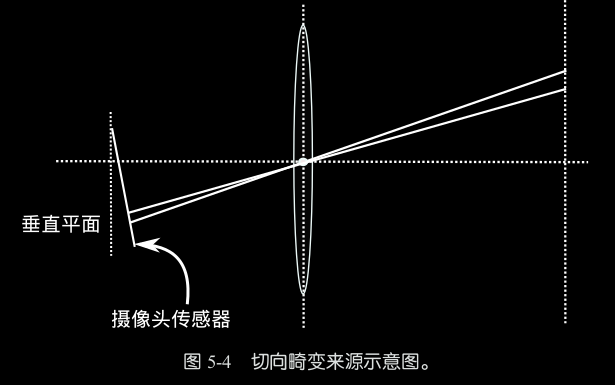
畸变校正

对于相机坐标系中的一点 P ，我们能够通过 5 个畸变系数找到这个点在像素平面上的正确位置：

  1. 将三维空间点投影到归一化图像平面。设它的归一化坐标为 [x, y]T 。
  2. 对归一化平面上的点计算径向畸变和切向畸变。Z值（深度）为1的假设平面

/posts/algorithm_knowledge_base/7_vslam/image%2025.png

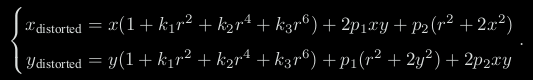
将畸变后的点通过内参数矩阵投影到像素平面，得到该点在图像上的正确位置。

相机标定

相机标定的目的

  1. 校正畸变：大多数相机镜头都会产生一定的畸变，常见的有径向畸变和切向畸变。标定可以获取相机的畸变系数，进而校正图像，使其符合真实场景。
  2. 获取内参矩阵：相机的内参描述了相机的焦距、主点位置等信息。内参矩阵在将三维空间的点投影到二维图像上时非常重要。
  3. 获取外参矩阵：外参描述了相机在三维空间中的位置和姿态，通常以旋转矩阵和位移向量表示。外参矩阵可以用于计算相机与世界坐标系的关系。

zhuanlan.zhihu.com

张正友标定法标定相机的内外参数的思路如下：

将世界坐标系固定于棋盘格上，则棋盘格上任一点的物理坐标W=0，任一角点的U、V坐标也已知，最少4个角点就可以求解Homography矩阵。

1）、求解内参矩阵与外参矩阵的积，即H；

2）、求解内参矩阵K；

3）、求解外参矩阵T，KT=H；

4）、求解畸变参数。

视觉里程计

特征点法、光流法（灰度不变假设）

https://blog.csdn.net/qq_41839222/article/details/86483071

/posts/algorithm_knowledge_base/7_vslam/image%2026.png

视觉里程计（Visual Odometry，VO）是一种基于图像的技术，通过分析连续图像帧来估计相机（或移动设备）的运动轨迹。视觉里程计广泛应用于机器人、自动驾驶、增强现实（AR）和虚拟现实（VR）等领域，帮助设备在没有GPS或其他定位系统的环境中实现自我定位和导航。

视觉里程计的基本原理

视觉里程计利用相机捕获的连续图像帧中的视觉信息，通过特征提取和匹配来计算相机在空间中的位姿变化。主要的流程通常包括以下几个步骤：

  1. 特征提取：在图像中检测关键特征点，常用的特征检测算法有SIFT、SURF、ORB等。这些特征点可以用来跟踪相机运动。
  2. 特征匹配：在相邻图像帧中，匹配提取的特征点，得到每个特征点在不同帧中的对应关系。
  3. 估计运动（姿态估计）：通过匹配的特征点，使用PnP、ICP（Iterative Closest Point）或双目三角测量等方法计算相机的姿态变化，即位移和旋转（外参）。
  4. 优化和滤波：使用优化算法（如Bundle Adjustment）来最小化重投影误差，提高运动估计的精度。对于长时间运行的系统，还可以加入滤波算法（如卡尔曼滤波、粒子滤波）来提高系统的鲁棒性。

视觉里程计的分类

视觉里程计根据使用的图像传感器类型和特征提取方式可分为以下几类：

  1. 单目视觉里程计
    • 使用单个相机，通常依赖特征点的运动来估计相机的位姿变化。
    • 优点：硬件要求低，计算相对简单。
    • 缺点：由于缺少深度信息，精度有限，依赖于图像特征点的质量。
  2. 双目视觉里程计
    • 使用双目相机，利用双目视差来获取三维深度信息。
    • 优点：可以直接获取深度信息，更精确地估计位姿变化。
    • 缺点：硬件要求高于单目视觉。
  3. RGB-D视觉里程计
    • 使用RGB-D相机（如Kinect）获取带有深度信息的图像。
    • 优点：直接获取深度信息，适用于室内环境。
    • 缺点：受光线影响大，通常只适用于近距离场景。
  4. 特征点法与直接法
    • 特征点法：通过检测和跟踪图像中的特征点，计算相机的运动。常用算法有ORB-SLAM、LDSO等。
    • 直接法：直接利用图像灰度信息进行配准，如DSO（Direct Sparse Odometry）。在光线稳定、纹理丰富的情况下，直接法效率更高。

常用的视觉里程计算法

  1. ORB-SLAM：
    • 基于特征点的SLAM（Simultaneous Localization and Mapping）方法，采用ORB特征，适合于多种类型相机。ORB-SLAM包含回环检测和重定位等模块，非常适合长期运行。
  2. LSD-SLAM：
    • 基于稀疏直接法的SLAM方法，使用图像灰度值进行位姿估计，适合在低纹理场景下运行。主要用于单目相机。
  3. DSO（Direct Sparse Odometry）：
    • 直接法的视觉里程计，通过稀疏图像配准直接估计相机位姿，在非特征丰富的场景中表现良好，且计算速度较快。
  4. VINS-Mono / VINS-Fusion：
    • 基于因子图优化的视觉里程计算法，融合IMU（惯性测量单元）数据，提升了单目相机在三维空间中的定位精度，特别适用于动态环境中。

2d-2d 对极几何

https://www.cnblogs.com/narjaja/p/10768179.html

通过二维图像点的对应关系，恢复出在两帧之间摄像机的运动

/posts/algorithm_knowledge_base/7_vslam/image%2027.png

对极约束简洁地给出了两个匹配点的空间位置关系。相机位姿估计问题变为以下两步：

  1. 根据配对点的像素位置求出 E 或者 F （都可以8点法求解）。
  2. 根据 E 或者 F 求出 R, t。
    由于 E 和 F 只相差了相机内参，而内参在 SLAM 中通常是已知的 ，所以实践当中往往使用形式更简单的 E。

/posts/algorithm_knowledge_base/7_vslam/image%2028.png

                                      x是归一化平面上的坐标，p是像素坐标。

基础矩阵F

/posts/algorithm_knowledge_base/7_vslam/image%2029.png

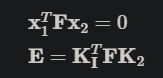
基础矩阵是一个 3×3 的矩阵，定义了在两个视图中对应点之间的约束关系。给定两个视图中的一个对应点对 (x,x′)，它们满足以下关系：

                                                   x′TFx=0

其中：

  • x和 x′ 分别是图像1和图像2中的对应点的齐次坐标。

  • F是基础矩阵，描述两个图像之间的对应关系，具有 7 个自由度

                            （*detF*=0的约束、尺度等价性各减去一个自由度）。

基础矩阵的作用是将图像1中的点通过约束关系映射到图像2中相应的极线，建立点和极线的关系。由于基础矩阵不依赖于相机内参，因此它可以应用于任意两个视图，适用于未标定的摄像机。8点法求解

本质矩阵E

不包含内参

本质矩阵 E = t∧ R。它是一个 3 × 3 的矩阵，内有 9 个未知数

平移向量 t 对应的反对称矩阵 t∧ 与旋转矩阵 R 的乘积

5个自由度（平移和旋转各有 3 个自由度，尺度等价性减去1个自由度）

8点法求解（最少5点）

/posts/algorithm_knowledge_base/7_vslam/image%2030.png

系数矩阵是根据对 e 的多项式进行拆分得到的

再对E进行SVD分解恢复R,t

单应矩阵H

/posts/algorithm_knowledge_base/7_vslam/image%2031.png

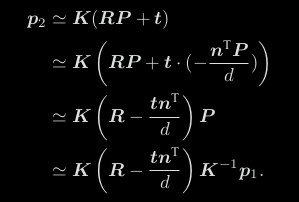
p2 ≃ Hp1 . nT是平面P的法向量，d是平面常数项参数

纯旋转或特征点在同一平面

/posts/algorithm_knowledge_base/7_vslam/image%2032.png

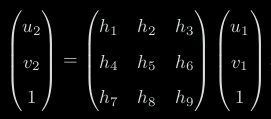
自由度为 8 的单应矩阵可以通过 4 对匹配特征点算出 DLT求解

可分解出R、t 数值法或解析法

自由度

  • 单应矩阵有 8 个自由度。尽管它包含 9 个元素 hij，但由于其定义是 up-to-scale 的（即在同一个变换下，矩阵的所有元素乘以一个非零常数仍然描述相同的单应性变换），所以只需要 8 个独立参数来确定这个矩阵。
  • 为了固定尺度，一般将 h33 归一化为 1 或将矩阵整体除以某一个元素，以便矩阵变换唯一确定。

3d-2d PnP

Perspective-n-Point

通过一组已知的三维点及其在二维图像中的投影点来确定相机姿态（位姿，即旋转和平移）的算法。

https://www.zywvvd.com/notes/study/camera-imaging/pnp/pnp/

PnP问题的定义

给定：

  1. n个三维点的坐标：在物体坐标系中，这些点的三维坐标已知，表示为(Xi​,Yi​,Zi​)。
  2. n个二维图像点：这些三维点在图像平面上的投影位置已知，表示为(xi​,yi​)。
  3. 相机内参矩阵：已知相机的内参矩阵K，包括焦距和主点位置等参数。内参未知时可尝试UPnP或同时估计内外参的方法，但这些方法通常比已知内参的PnP问题更复杂，并且可能对噪声和初始化更敏感。

目标是求解相机的外参，即相机相对于物体的旋转矩阵 R 和平移向量 t，将三维点投影到图像上。

PnP问题的求解步骤

  1. 模型建立：在相机坐标系中，根据相机内参矩阵和外参矩阵，得到3D点到2D点的投影关系公式。

    /posts/algorithm_knowledge_base/7_vslam/image%2033.png

  • 其中 K为相机内参矩阵，[R∣t][R | t][R∣t] 为外参矩阵。
  • 方程求解：根据不同方法（如EPnP、RANSAC+PnP等）求解出R 和 t。
  • 优化与精确化：通常会进行非线性优化（如Levenberg-Marquardt），以最小化重投影误差，进一步精确外参矩阵。
  • 验证与应用：将解出的姿态应用到实际场景中，可以得到相机的位置和方向。

DLT（Direct Linear Transformation）

空间点P，齐次坐标为 P = (X, Y, Z, 1)T，投影到特征点 x1 =(u1 , v1 , 1)T （归一化平面，与图像点只差一个内参，因此可等效替代）

定义增广矩阵 [R|t] 为一个 3 × 4 的矩阵，包含了旋转与平移信息

/posts/algorithm_knowledge_base/7_vslam/image%2034.png

12个未知数，一对匹配点提供2个关于t的线性约束

  • 在点数多于6个的情况下，通过线性方法直接求解PnP问题。DLT方法虽然简单，但易受噪声影响，因此通常用于粗略估计。
  • 优势：实现简单，但对噪声敏感。

P3P

https://www.cnblogs.com/mafuqiang/p/8302663.html

/posts/algorithm_knowledge_base/7_vslam/image%2035.png

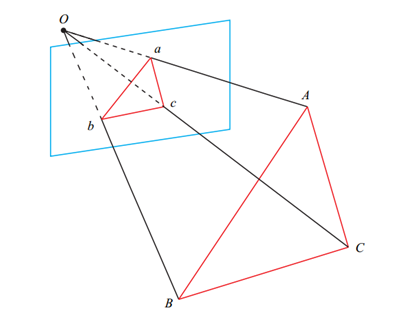
将P3P问题转换为ICP问题求解，核心是求解3个2d点在当前相机坐标系下的3d坐标

需要求解二元二次方程，最少需要一个点，还需要额外的第4个点验证

方程的建立是依据余弦定理

/posts/algorithm_knowledge_base/7_vslam/image%2036.png

Bundle Adjustment

定义于李代数上的非线性最小二乘问题

最小化重投影误差

没有回环也可以做局部BA

光束法平差的基本原理

  1. 已知条件：

    • 多个视角下的图像以及对应的特征点。
    • 每个视角的相机内参（如焦距、主点位置、畸变系数）和外参（位置和朝向）。

  2. 目标：

    • 优化相机的内外参数和三维点的位置，使得通过相机投影回到图像的三维点与实际检测到的二维特征点之间的重投影误差最小。

  3. 重投影误差：

    • 重投影误差是指将三维点通过相机模型投影到图像平面后，计算得到的二维点与实际检测到的二维特征点之间的差距。这个误差通常用平方和来表示：

    /posts/algorithm_knowledge_base/7_vslam/image%2037.png

    其中，pij是第j个相机观察到的第i个三维点的实际图像位置，π是投影函数，Rj和tj是第j个相机的旋转和位移。

3d-3d ICP

zhuanlan.zhihu.com

两种常见的点云配准方法ICP&NDT

点云配准算法 求解R,t

icp、ndt

没有一个明确的最少点数要求，但为了确保ICP算法的鲁棒性和准确性，通常推荐使用尽可能多的点，同时保证点云的均匀分布和质量。

不涉及二维到三维，因此不需要内参

三角测量（空间前方交会 已知观察未知）

https://baike.baidu.com/item/%E7%A9%BA%E9%97%B4%E5%89%8D%E6%96%B9%E4%BA%A4%E4%BC%9A

由立体像对左右两影像的内、外方位元素和同名像点的影像坐标测量值来确定该点的物方空间坐标。

https://gutsgwh1997.github.io/2020/03/31/%E5%A4%9A%E8%A7%86%E5%9B%BE%E4%B8%89%E8%A7%92%E5%8C%96/

/posts/algorithm_knowledge_base/7_vslam/image%2038.png

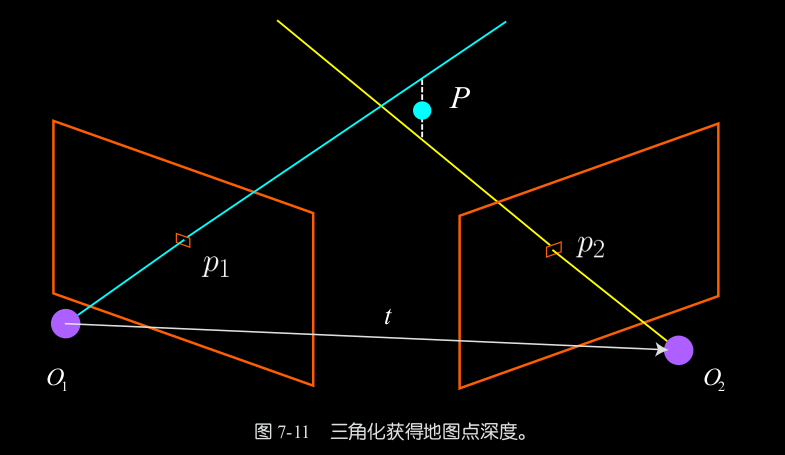
已知夹角和基线（R和t）、内参矩阵以及特征点像素坐标p1、p2，求解深度s1、s2

s1 x1 = s2 Rx2 + t.

orb-slam2

单目、双目、RGBD

/posts/algorithm_knowledge_base/7_vslam/image%2039.png

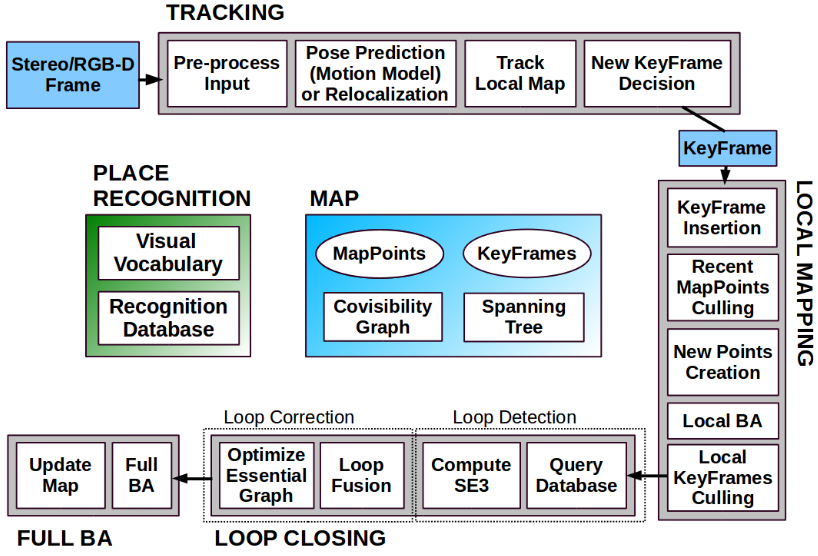
主线程 创建了System类型的对象，核心控制器，负责调度

四个并行子线程

轨迹追踪

局部建图

回环检测 全部完成后会开启全局BA线程

可视化稀疏地图

Updated on 2025-04-16
 3d, Slam
Back | Home