3DGS

fjyu95 included in 三维重建

2024-11-08 7397 words 15 minutes

Contents

技术总览

GitHub - 3D Gaussian Splatting for Real-Time Radiance Field Rendering

3D Gaussian Splatting

球谐系数与球面高斯

【转载】3D Gaussian Splatting中的数学推导

3D建模零門檻！以照片生成場景的3DGS技術解析

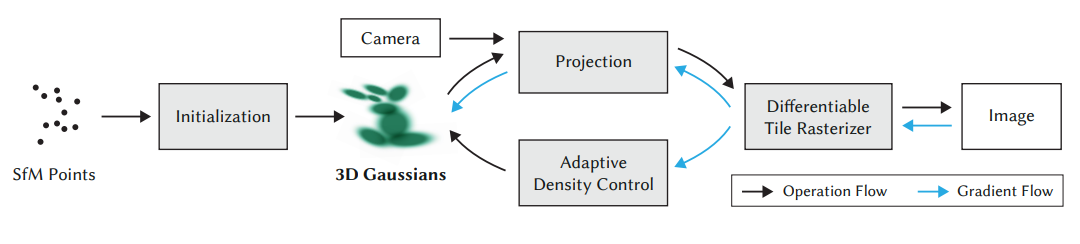
3DGS使用随机梯度下降法进行训练。步骤如下：

SfM Points：首先利用运动恢复结构技术（Structure from Motion，SfM），从一组2D相片中找到不同照片中叠合的特征点，来估计出初步的3D点云及相机位置，程式码中是透过调用COLMAP库来完成。
Initialization：透过SfM获得的点云及数据进行初始化，算出各个高斯椭球的位置、形状、颜色、透明度等参数。
Projection：将每一颗高斯椭球，根据它们与各个相机位置的距离（深度），由近到远排序进行投影；代码中是将中心点座标去跟变换矩阵、协方差矩阵等数据进行运算，就能将三维空间中的高斯分布转换到二维的平面上。
Differentiable Tile Rasterizer：透过可微光栅化渲染（即前文提及的「Splatting」得到一张张2D图像（即流程上的「Image」）。
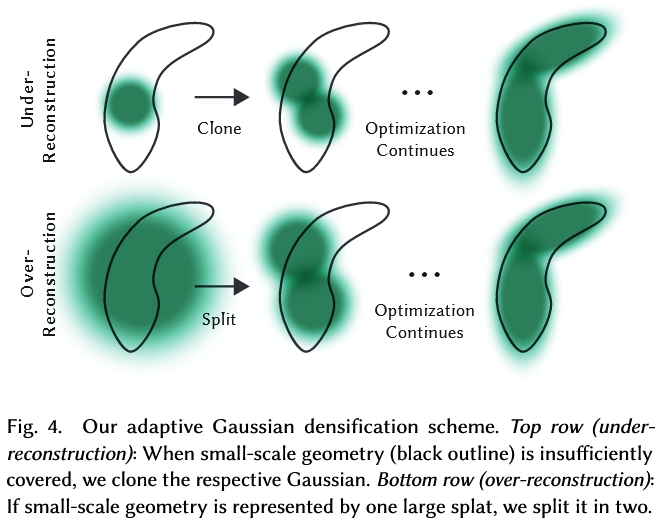
Adaptive Density Control：根据步骤4.所获得之渲染2D图像（即流程上的「Image」）与Ground Truth图像（原先上传的照片）之间的差异，计算出loss值，并将loss值沿蓝色箭头方向回传。蓝色箭头向上即更新3D高斯椭球的参数，向下则送入自适应密度控制来更新高斯椭球的密度，如将小颗的高斯克隆成两颗、将大颗的高斯分裂两小颗等，以更好地拟合照片中的细节。

全文翻译

https://blog.csdn.net/m0_38068229/article/details/137171860

https://blog.csdn.net/m0_52065936/article/details/132805104

算法原理

3D Gaussian Splatting是一种用于三维重建的算法，其主要思路是使用三维高斯分布来表示场景中的点，实现高效且连续的场景重建。与传统的NeRF（Neural Radiance Fields）等方法相比，3D Gaussian Splatting在渲染效率和重建速度方面具有显著优势。以下是3D Gaussian Splatting算法的核心原理：

1. 高斯分布表示3D点云

在3D Gaussian Splatting中，场景中的每个点由一个三维的高斯分布来表示，这个分布通常由位置、颜色、大小和方向参数来描述。
与点云中的离散点不同，3D高斯分布可以形成一个连续的概率分布函数（PDF），使得这些点具有空间延展性和模糊性。
通过这种分布，渲染时可以避免单独的采样点，仅需计算每个像素位置上高斯分布的叠加效果。

2. 投影与融合

在渲染阶段，3D高斯分布的中心点会投影到图像平面，并生成二维的“splat”（点状）表示。
这些splat在像素平面上叠加，并根据其权重和透明度信息融合，形成最后的渲染结果。
这种投影方法能够将高斯体积投影到图像平面，减少了体积渲染中的高维采样步骤。

3. 权重与透明度

3D Gaussian Splatting使用alpha合成方法来处理不同的透明度和颜色信息。
透明度是根据和椭圆中心的距离直接计算的吗？
每个高斯体积根据其距离、方向和视角影响渲染中的权重和透明度，使得最终的图像具有真实的深度感和透明效果。

4. 优化与加速

该算法通常结合了多层次优化技术，包括多尺度表征、渐进式细化等。
在具体实现中，还可以使用GPU加速以处理高分辨率点云和快速渲染，使得实时应用成为可能。

5. 应用场景

3D Gaussian Splatting适用于场景重建、虚拟现实（VR）渲染、视频游戏以及电影制作等需要高质量3D渲染的领域。
它的渲染速度相对较快，并且具有较强的连续性，非常适合需要快速场景预览和即时效果的应用。

与NeRF的对比

3D Gaussian Splatting算法与NeRF相比，在渲染效率上更具优势，因为NeRF需要对整个三维空间进行稠密采样，而高斯分布可以直接形成连续表示。
相较于NeRF的体积渲染，3D Gaussian Splatting在减少采样点的同时仍能保留图像质量，因此更适合实时渲染和场景重建任务。

通过3D Gaussian Splatting的高效三维点表示与投影融合策略，这一算法能够在保持较高图像质量的同时，实现快速且连续的3D场景渲染。

算法理解

3D Gaussian点定义：

关键参数：

x：空间位置

 **增加或减少Gaussian点，利用位置梯度**

Σ：三维高斯分布的协方差矩阵，表示椭球的缩放和旋转

  Gaussian点的参数只有Σ，其决定了椭球的形状和对称轴方向，不决定椭球的位置。

  训练过程就是用渲染图和原图比较计算视野中高斯点的矩阵Σ的梯度，然后梯度下降调Σ。

Σ=RSSTRT

α：不透明度（中心为1，越往四周越透明）

Color：用球谐系数来表示每个高斯的颜色，不同视角颜色不同。16X3（RGB）矩阵

       球谐系数是一组表示任意函数的“基函数”的系数，（`sh_degree`+1）^2*3

3DGS原理解析

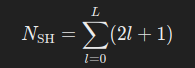
3DGS算法中定义一个3D Gaussian的参数：

Position (Mean μ): location (XYZ)
Covariance Matrix (Σ): rotation and scaling
Opacity (α): Transparency，这个参数会在alpha blending阶段时与相乘
Color (RGB) or Spherical Harmonics (SH) coefficients

使用随机梯度下降SGD，对Mean、Covariance Matrix、α、Color进行参数优化。

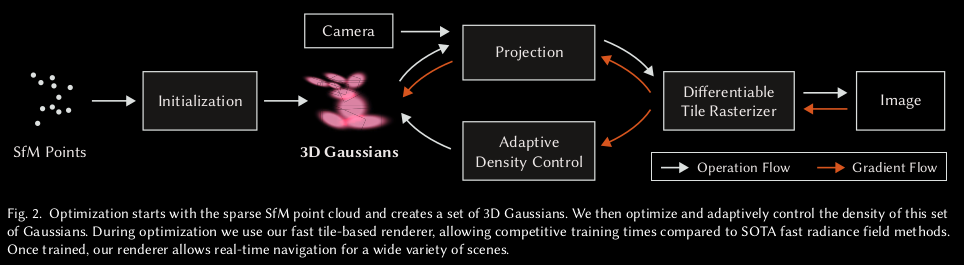
使用SfM(Structure from Motion)初步创建一组point cloud
将步骤1创建的point cloud转换为3D Gaussian
使用SGD训练。训练过程是将3D Gaussian使用differentiable Gaussian rasterization方法rasterize到图像上，通过生成图像与真实图像来计算loss值，调整参数，实现自动densification调整
Differentiable Gaussian Rasterization

可以简单将其概括为如下几步：

录一段视频或者拍一组不同角度的照片，用一些技术（例如SfM）估计点云。或者直接随机初始化一组点云。
点云中的每一个点，代表着一个三维的高斯分布，所以除了点的位置（均值）以外，还有协方差，以及不透明度，以及颜色（球谐系数）。直观可以理解为一个”椭球体“。
将这些椭球体沿着特定的角度投影到对应位姿所在的投影平面上，这一步也叫“splatting“，一个椭球体投影到平面上会得到一个椭圆（代码实现时其实是以长轴为直径的圆），然后通过计算待求解像素和椭圆中心的距离，我们可以得到不透明度（离的越近，说明越不透明）。每个椭球体又各自代表自己的颜色，这是距离无关的。于是就可以进行alpha compositing，来合成颜色。然后快速的对所有像素做这样的计算，这被称作”快速可微光栅化“。
于是可以得到整个图片，再和ground truth比较，得到损失，然后梯度反传，随机梯度下降，进行优化。

源码解读

3dgs 源码解读

Q&A

1、3d高斯点如何映射到的2d平面？

透视投影 近大远小，将远处的平面挤压之后再做正交投影

正交投影 相机无限远的特殊情况，渲染时直接把z轴扔掉

2、2d上同一个像素点覆盖的时候3d高斯点颜色如何合成？

球谐系数的使用不同视角有不同颜色值

一组球面上的基函数，把高斯块上面的点的颜色建模成了一个球谐函数

α-blending

3、16*16瓦片的作用

Optimized GPU Rendering

将屏幕分为16*16的tiles，保留99%在视锥里的Gaussians，
给每个Gaussian一个key=depth+ID，然后将Gaussians进行GPU Radix Sort，得到了每个tile里根据depth排序的Gaussian列表，
每个tile分配thread block，每个block先load到shared memory，对于每个pixel，累积color和alpha，达到饱和时停止。

4、损失函数及优化算法？

 The loss function is L1 combined with a D-SSIM term:

也可以包括Depth regularization

优化算法：

Adam
计算梯度的一阶矩（均值）和二阶矩（方差）来调整学习率

1
2
  if self.optimizer_type == "default":
		  self.optimizer = torch.optim.Adam(l, lr=0.0, eps=1e-15)

5、是否包含神经网络

3D Gaussian Splatting本身并不包含神经网络。它是一种基于物理的渲染技术，用于在3D场景中模拟光线的传播和散射。在这种技术中，物体被表示为大量的小颗粒（splat），每个颗粒都对应一个高斯函数，用于描述光线的分布和散射。
然而，3D Gaussian Splatting可以与神经网络结合使用，以实现更高效、更真实的渲染效果。例如，可以使用神经网络来学习场景的几何结构、材质属性和光照条件，从而生成更准确的高斯函数参数。此外，神经网络还可以用于加速渲染过程，通过学习输入图像和输出图像之间的映射关系，实现实时或近实时的渲染。
总的来说，3D Gaussian Splatting本身不包含神经网络，但可以与神经网络结合使用，以提升渲染效果和效率。

在标准的 3D Gaussian Splatting 方法中，并未直接使用神经网络。它的核心是一种基于数学建模和传统计算机图形学的渲染技术，通过显式的高斯分布建模和投影来实现高效的点云或稀疏体积数据渲染。不过，近年来一些改进方法可能会结合神经网络进行优化。

1. 传统 3D Gaussian Splatting 的原理

(1) 核心流程

高斯分布建模：每个 3D 点被建模为各向异性高斯分布（包含位置、协方差矩阵、颜色、透明度等参数）。
投影与积分：将 3D 高斯分布投影到 2D 屏幕空间，通过解析积分或近似方法计算像素颜色。
Alpha 混合：根据深度排序对重叠的高斯分布进行透明度混合，生成最终图像。

(2) 技术特点

显式参数化：所有参数（位置、协方差、颜色）均为显式定义，无需神经网络隐式表示。
优化依赖：通过非线性优化（如梯度下降）调整高斯参数，而非神经网络的端到端训练。

2. 与神经网络的结合方向

虽然传统方法本身不依赖神经网络，但在近年研究中，3D Gaussian Splatting 的改进版本可能引入神经网络，例如：

(1) 参数优化加速

神经网络辅助初始化：
使用神经网络预测初始高斯参数（如协方差矩阵、颜色），替代随机初始化，加速收敛。
可微分渲染：
将 Gaussian Splatting 的渲染过程设计为可微分模块，与神经网络联合训练，优化几何和外观。

(2) 动态场景建模

形变场预测：
用神经网络预测动态场景中高斯参数的时变形变（如运动轨迹），替代传统物理模拟。
神经辐射场混合：
结合 NeRF 的隐式辐射场与 Gaussian Splatting 的显式表达，提升渲染质量（如 3D-GS+NeRF 混合方法）。

3. 与 NeRF 的对比

维度	3D Gaussian Splatting	NeRF
表示形式	显式高斯分布	隐式神经辐射场
是否需要 NN	否（传统方法）	是（MLP 网络建模）
渲染速度	实时级（>30 FPS）	分钟级（需逐像素采样）
内存占用	较高（存储显式参数）	较低（仅存储网络权重）
动态场景支持	需额外扩展（如形变场）	需时序建模（如 NSFF、DyNeRF）

4. 典型应用案例

(1) 纯 Gaussian Splatting

大规模点云渲染：如 LiDAR 数据可视化。
实时 AR/VR：依赖高效光栅化，无需神经网络推理。

(2) 神经网络增强版

高质量表面重建：用神经网络优化高斯分布参数，填补空洞（如 Neural Splatting）。
动态对象建模：结合 Transformer 预测高斯参数的动态变化。

总结

传统 3D Gaussian Splatting：不依赖神经网络，基于数学显式建模，适合实时渲染。
改进版本：可能引入神经网络以优化参数、处理动态场景或增强细节，但核心仍是高斯投影框架。

若场景建模需要实时性且无需复杂细节，传统方法足够高效；若追求电影级质量或动态建模，可探索与神经网络的混合方案。

6、相机视角表示

在 3D Gaussian Splatting 中，相机视角的表示非常重要，因为它直接影响渲染结果。相机视角决定了你如何从不同的角度观察和渲染3D场景中的高斯点（splats）。为了有效地在 3D 空间中进行渲染和视觉化，我们需要用某种方式来表示和操作相机的视角。

相机视角的基本表示

相机的视角通常由以下几个元素来描述：

相机位置（Camera Position）：
- 这是相机在世界坐标系中的位置。它决定了相机从哪个位置观看场景。
- 在3D渲染中，相机的位置通常用一个 3D 向量表示，例如。
  $\mathbf{C} = (x, y, z)$
视线方向（Camera Orientation or Look-At）：
- 视线方向是指相机正在观察的方向。它通常通过相机朝向的单位向量来表示。
- 可以通过欧拉角（Pitch, Yaw, Roll）或者四元数来描述相机的旋转，或者直接通过一个目标点来定义相机的“朝向”（Look-at）。
相机的投影矩阵（Projection Matrix）：
- 投影矩阵定义了从相机到场景的投影方式，通常是正交投影（Orthographic Projection）或透视投影（Perspective Projection）。
- 透视投影会根据物体到相机的距离进行缩放，而正交投影则保持物体的大小不变。
视场（Field of View, FOV）：
- 视场定义了相机的视角，即相机能够看到的范围。通常用角度来表示，例如水平视角或者垂直视角。
- FOV 和投影矩阵一起决定了渲染时场景的可见区域。

在 3D Gaussian Splatting 中的具体实现

在 3D Gaussian Splatting 中，相机视角主要用来决定如何渲染从高斯点表示的场景。具体来说，相机的视角与高斯点的投影相关，影响点云或高斯点的呈现方式。为了在 GPU 上进行渲染，通常需要对相机的视角进行有效表示，并将其与点云数据结合，以下是一些关键步骤：

高斯点与相机的关系：
- 在 Gaussian Splatting 中，每个高斯点都有一个位置、大小和权重。当相机视角发生变化时，点云数据会根据相机的位置和方向进行重新投影，显示在屏幕上的位置也会发生变化。
- 高斯点的大小、透明度、颜色等信息可能会根据视角进行动态调整。例如，当一个高斯点靠近相机时，它可能看起来更大，而远离相机的点则看起来更小。
相机矩阵和坐标变换：
- 视图矩阵（View Matrix）：用于将世界坐标系中的点转换为相机坐标系中的点。这通常通过旋转和平移矩阵来实现，确保相机能够正确地观察场景。
- 投影矩阵（Projection Matrix）：用于将 3D 相机坐标系中的点投影到 2D 屏幕上。这个矩阵将相机坐标系的点转换为裁剪空间中的点，并根据视场和近远裁剪平面进行缩放。
- 这两个矩阵共同定义了如何在屏幕上呈现高斯点。
视角影响的渲染：
- 在渲染过程中，相机的视角决定了如何从 3D 空间中的高斯点投影到 2D 屏幕上。如果相机移动或旋转，视角就会变化，导致不同的高斯点投影到屏幕上的位置变化。
- 相机的变化也会影响高斯点的透明度和权重，尤其是对于远离相机的点，通常需要通过透明度衰减来模拟物体远离视点时的视觉效果。
视角变化和高斯点的自适应调整：
- 高斯点的表现可能不仅仅依赖于相机视角，还可能根据相机的视角自适应调整。比如在某些情况下，视角的改变可能导致对近处或远处物体的不同处理，例如近处物体显示更多的细节或较大尺寸的高斯点。

相机视角表示的实际应用

在 3D Gaussian Splatting 中，一种常见的做法是通过一个基于视角的渲染管线来处理相机视角。这个管线包括以下几个步骤：

高斯点的投影计算：
- 根据当前的相机位置、朝向以及视角信息，将 3D 高斯点投影到 2D 屏幕空间中。每个点的大小和权重也可能根据视角进行调整。
动态调整高斯点的渲染属性：
- 例如，根据相机距离调整高斯点的大小，或者根据光照和视角调整颜色和透明度。
- 高斯点的权重也可能基于视角变化来调整，确保在不同的视角下渲染效果自然。
GPU 加速渲染：
- 相机视角的信息常常会通过矩阵传递给渲染引擎，在 GPU 上进行高效的视角转换和渲染。CUDA 或 OpenGL 等技术常常用于加速这些计算。

视角表示与深度学习中的结合

在一些 基于深度学习的 3D Gaussian Splatting 方法中，相机视角的表示可以与神经网络模型相结合。例如，在通过多视角图片重建 3D 场景的任务中，神经网络可以根据多个视角的图像数据来学习高斯点的空间分布和渲染参数。在这些方法中，相机视角可能被输入到网络中，作为条件来影响高斯点的生成和渲染效果。

总结

在 3D Gaussian Splatting 中，相机视角的表示包括位置、朝向、投影矩阵、视场等因素，直接影响渲染结果。
相机视角决定了如何将 3D 高斯点投影到 2D 屏幕，并且影响高斯点的大小、透明度、颜色等渲染属性。
相机矩阵（视图矩阵和投影矩阵）用于将 3D 点转换到相机坐标系中，并最终映射到屏幕空间。
在现代的基于神经网络的 3D 渲染中，相机视角的表示可能会与神经网络结合，进一步优化和生成更加真实的 3D 场景。

code

1
2
3
4
5
6
7
# camera_utils.py
    return Camera(resolution, colmap_id=cam_info.uid, R=cam_info.R, T=cam_info.T, 
                  FoVx=cam_info.FovX, FoVy=cam_info.FovY, depth_params=cam_info.depth_params,
                  image=image, invdepthmap=invdepthmap,
                  image_name=cam_info.image_name, uid=id, data_device=args.data_device,
                  train_test_exp=args.train_test_exp, is_test_dataset=is_test_dataset, is_test_view=cam_info.is_test)
 相机视角是通过R、T、FOV等来表达的

查看器

https://projects.markkellogg.org/threejs/demo_gaussian_splats_3d.php

https://playcanvas.com/supersplat/editor

https://ernestchu.github.io/splat/

延伸思考

1、3DGS vs. 航空摄影测量

3DGS（3D Gaussian Splatting）与传统航空摄影测量建模效果对比

3D Gaussian Splatting（3DGS）是近年来兴起的一种基于点云和概率分布的实时渲染技术，而传统航空摄影测量建模则是基于多视角几何和密集匹配的经典方法。二者在建模原理、效果表现和应用场景上存在显著差异，以下是详细对比：

1. 核心原理对比

技术	传统航空摄影测量建模	3DGS（3D Gaussian Splatting）
建模基础	基于多视角影像的几何重建（SFM + MVS）	基于概率分布的点云表示（高斯分布参数化场景）
数据输入	高重叠率航拍影像 + POS数据（位置姿态信息）	多视角影像（可无需精确位姿）
输出形式	密集点云 → 网格模型（Mesh） + 纹理贴图	概率化点云（高斯椭球体） + 实时渲染
计算核心	几何匹配、三角测量、全局优化	概率密度建模、可微分渲染、GPU加速优化

2. 建模效果对比

(1) 几何精度

传统摄影测量
- 优势：依赖精确的影像匹配和空中三角测量，几何精度高（可达厘米级），适合工程测绘和地形建模。
- 劣势：对影像质量、重叠率和光照一致性要求高，复杂场景（如植被、透明物体）易出现孔洞或噪声。
3DGS
- 优势：通过高斯分布建模，能更自然地表达复杂表面（如树叶、毛发），细节表现更柔和。
- 劣势：几何精度依赖概率优化，绝对精度较低（适用于视觉展示而非测绘）。

(2) 视觉效果

传统摄影测量
- 依赖纹理贴图，模型表面色彩真实但可能因光照差异出现接缝。
- 静态模型，不支持动态光照或实时交互。
3DGS
- 基于概率体渲染，支持动态光照和视角插值，视觉过渡更平滑。
- 实时渲染性能强（如游戏引擎集成），适合VR/AR应用。

(3) 处理效率

传统摄影测量
- 流程复杂：空中三角测量 → 密集匹配 → 网格化 → 纹理映射，耗时长（小时级）。
- 依赖高性能CPU/集群计算。
3DGS
- 端到端优化，支持GPU加速，训练和渲染速度更快（分钟级到实时）。
- 对硬件要求较低（消费级显卡即可）。

3. 适用场景对比

场景	传统摄影测量	3DGS
地形测绘	✅ 高精度DEM/DSM生成，工程测量	❌ 几何精度不足
文化遗产保护	✅ 高保真静态模型（如古建筑扫描）	✅ 动态展示、虚拟漫游
影视/游戏	❌ 静态模型，后期需手动优化	✅ 实时渲染、动态光照支持
动态场景	❌ 仅支持静态场景	✅ 可扩展至动态物体（如人物、车辆）
大规模场景	✅ 分块处理技术成熟	❌ 显存限制，适合中小场景

4. 优缺点总结

技术	优点	缺点
传统摄影测量	- 高几何精度 - 大场景支持成熟	- 流程复杂耗时 - 动态效果差
3DGS	- 实时渲染 - 细节自然 - 动态扩展性强	- 几何精度低 - 显存限制大场景

5. 未来趋势

传统摄影测量：向自动化、AI辅助优化（如语义分割修复孔洞）发展。
3DGS：与NeRF（神经辐射场）结合，提升几何精度和大场景支持能力。

选择建议

优先传统摄影测量：测绘、工程、考古等需要高精度几何数据的场景。
优先3DGS：影视特效、游戏开发、虚拟展厅等注重实时交互与视觉效果的领域。

两种技术并非完全替代，未来可能通过混合建模（如3DGS优化表面细节 + 摄影测量保障几何精度）实现更全面的三维重建。